California Moves Closer to Passing New Guidelines for Teaching Math

The State Board of Education is poised to approve a nearly 1,000-page guidance for math instruction this week with the ambitious, much-contested goal of transforming how math is taught in California, where only a third of students ­— and 1 in 5 low-income students — met standards in the latest state standardized test.

With the adoption of new textbooks, it may take years of intensive teacher training on a magnitude the state has not funded in decades before it becomes clear whether the revised Mathematics Framework for California Public Schools will move the needle of student engagement and achievement. Many teachers are confident it will, but there are skeptics.

The revised framework is nearly four years in the making. The third and likely last version, in response to more than 900 comments and petitions pro and con, took 14 months to complete. It was drafted by a new set of writers connected with the Region 15 Comprehensive Center of WestEd, the San Francisco-based research and service organization contracted by the California Department of Education.

The state board released the new draft on June 26; it accepted comments only through noon on July 7. After a final hearing scheduled for Wednesday, the board is expected to pass it, perhaps with minor changes.

Among those who will urge the board to adopt the final draft is Kyndall Brown, a former high school math teacher who is the executive director of the state-funded California Mathematics Project Statewide Office. Saying he was pleased that the “spirit” of the framework remains intact, Brown added, “This is the most equity-focused math framework I have ever seen as an educator in California.”

“The biggest and strongest part of this framework are the chapters on teaching and structuring school experiences for equity and engagement,” he said. “The math ed community, the people I interact with on a regular basis, support the framework, and we are ready to move forward and get this implemented.”

The framework’s recommendations are voluntary, but they heavily influence districts’ and teachers’ decisions and serve as guidelines for textbook publishers. The first two drafts have stirred national interest, in part because California, with 5.8 million students, is the nation’s largest and most lucrative market for textbook publishers, who, the framework’s authors make clear (see Chapter 13), will have to hew to its guidelines to make the list of approved publishers.

But the proposed framework also adds another twist in the decades long debate over math instruction. Math traditionalists are warning that a proposed student-centered, inquiry-based, “big-ideas” driven instructional strategy, which de-emphasizes memorization and attention to procedures, will fail most students.

Thousands of university STEM professionals signed petitions criticizing a proposed high school pathway that appeared to favor data science over the traditional course sequence to calculus, which is required for college students majoring in science, technology, engineering and math. Parents of students with advanced math skills and 6,000 others who signed a related petition were angry that the framework discouraged districts from starting algebra in eighth grade. The early start would give students a leg up on fitting in calculus before high school graduation.

In response, the new writers did eliminate the call for a new data science pathway; instead, they wove data skills into math instruction throughout grade spans. They also made some effort to clear up confusion conflating courses in data literacy, which all 21st-century students need, with a more rigorous, math-intensive data science course that, together with calculus, would prepare students for a data science major in college.

What the framework didn’t discuss, however, is a related controversy roiling the University of California and California State University faculties over whether a growing list of UC-authorized data science courses, with minimal advanced math content, will leave students unprepared for math-intensive courses in college.

Last week, a committee of the UC faculty senate, called BOARS, which oversees high school course qualifications, publicly acknowledged it is having second thoughts on the approved courses. In a July 7 letter to the state board (PDF), the chair of BOARS asked that the revised framework delete references in the text and in a diagram (see below) indicating that data science courses can substitute as a math requirement for Algebra II. The letter indicated that BOARS planned to look into the issue further.

The writers of the latest revision rephrased or removed some citations of works in the prior version, on neuroscience and other topics. Some of the citations of work support the instructional methods promoted by math instruction experts, including Stanford University math education professor Jo Boaler, one of the original framework’s team of authors.

At least some critics who had hoped that a year of work would fix the numerous problems they raised remain dissatisfied. The most prolific, if not most influential of them, Brian Conrad, professor of mathematics and director of undergraduate studies in math at Stanford, once again called for rejection of the framework due to shortcomings he cited.

In a nine-page update of his dissertation-length critique from a year ago, he pointed to remaining citation misrepresentations, and inconsistencies that could lead to contradictory interpretations of the framework and data science issues. “Critical concerns remain, and the (framework) does not live up to the standards of a document that sets state-wide education policy,” he wrote in a public comment last week.

Philosophy intact

Most of the past year’s effort went into clarifying, shortening and reorganizing the massive document. The focus of rewriting was on a half-dozen chapters, including the first two, laying out how to develop positive mindsets about math, like the belief that all students can succeed in math, and use students’ diverse backgrounds as “cultural assets.” Vignettes useful for teachers that lengthened chapters were moved to an appendix.

Most significantly, the new draft didn’t retreat from its primary charge to make math engaging and relevant for the many students who, particularly once they hit middle school, see math as abstract and inaccessible. That was the guidance of focus groups of teachers, an advisory group of California educators called the Curriculum Framework and Evaluation Criteria Committee, and the state board.

Using “open, engaging tasks” and “inviting student questions and conjectures” will be among the classroom strategies the framework cites as ways to meet the needs of diverse students; another is to “teach toward social justice,” such as creating graphs of student homelessness or doing data analysis of air and ground pollutants by neighborhood.

“Teaching towards social justice is really about using activities and discussions that really highlight some of the inequities in the world,” Boaler said during a June 29 webinar with writers of the original draft following the release of the new draft.

Discouraging Algebra 1 in eighth grade

The earlier writers weren’t involved in the latest rewrite, but, during the webinar, they generally praised the result. Brian Lindaman, co-faculty director of the Center for Science and Mathematics Instruction at Chico State, and the lead of five authors of the earlier framework, said that based on the chapters he had read, “I have liked and appreciated the changes by and large,” including improvements in “the readability, the flow, the coherence of it.”

The revised framework also didn’t back off the previous recommendation that nearly all students shouldn’t take Algebra I until ninth grade. It does acknowledge that “some students will be ready to accelerate” into Algebra I in eighth grade, affording them greater access to advanced courses in high school. But those students should be tested for algebra readiness, and schools should consider offering them summer courses, like Bob Moses’ Algebra Project, which has successfully prepared underrepresented students for algebra, the framework states.

Districts have the authority to decide which students can take algebra in eighth grade; a 2015 state law, the Math Placement Act, requires districts to adopt objective criteria for placing students in math courses, and consistently apply their policies. But many districts will take their lead from the state.

To discourage widespread enrollment in eighth-grade algebra, the framework’s diagram laying out STEM and non-STEM course pathways omits eighth-grade algebra as an option. To justify its position, the framework cites California’s experience in the early 2000s, when the state pressured districts to offer eighth-grade algebra; studies showed many students were unprepared and ended up repeating the course, with no better outcome. “Success for many students was undermined,” the framework said.

But Conrad counters that the more recent experience in San Francisco Unified, forcing all students to learn algebra in ninth grade, “was a total failure, exacerbating the very inequities it aimed to prevent, and is especially misguided since this country faces a dire shortage of STEM professionals.”

A “common ninth-grade experience” in math also is a strategy to prevent tracking, the practice of identifying potentially advanced math students as early as elementary school. That can have the effect of stunting the self-image, aspirations and abilities of non-tracked students. These students, predominantly low-income Black and Hispanic children, tend to end up with the least inspiring curriculums and least experienced teachers, Brown said. The harmful effects of tracking, he said, are real.

“If we can wait to hold the tracking off until at least eighth grade, we’ve given more kids opportunities to stay on the pathway to get high-level math classes,” said Cole Sampson, a member of the education advisory group to the framework and administrator of professional learning and student support for the Kern County superintendent’s office.

But placing algebra-ready students into a heterogeneous classroom of students with a wide range of skills can compound the challenges for teachers. It also denies eighth graders ready for algebra a jump-start to high-school math. To get to calculus, they must now double up math courses, enroll in a summer course or take a challenging compression math course, with supplemental help if they’re lucky. For low-income students holding down jobs, the obstacles hindering acceleration can force them to abandon plans for a STEM concentration in college.

Shorter path to calculus

As an alternative to eighth-grade algebra, the framework recommends that a task force investigate whether eliminating redundancies in the content of current courses could reduce four courses — Algebra I, Geometry, Algebra II and Precalculus — to three and reach advanced math like calculus by senior year.

Brown is confident this could be done. Conrad is skeptical, noting the framework drafters have had three years to come up with an alternative and haven’t. Mathematics professor Katherine Stevenson, the director of developmental mathematics at CSU Northridge, finds herself in between: It won’t be possible to pare down a course sequence without first looking at the 2013 Common Core math standards through the lens of what standards students will need in 2030, and then redesign a course sequence based on those standards.

Most students don’t major in STEM in college or take calculus. The biggest challenge to high school math is to design courses that will enable students to “exercise choice about their futures” by, the framework says, providing them “more opportunities to make choices that reflect their interests and aspirations.”

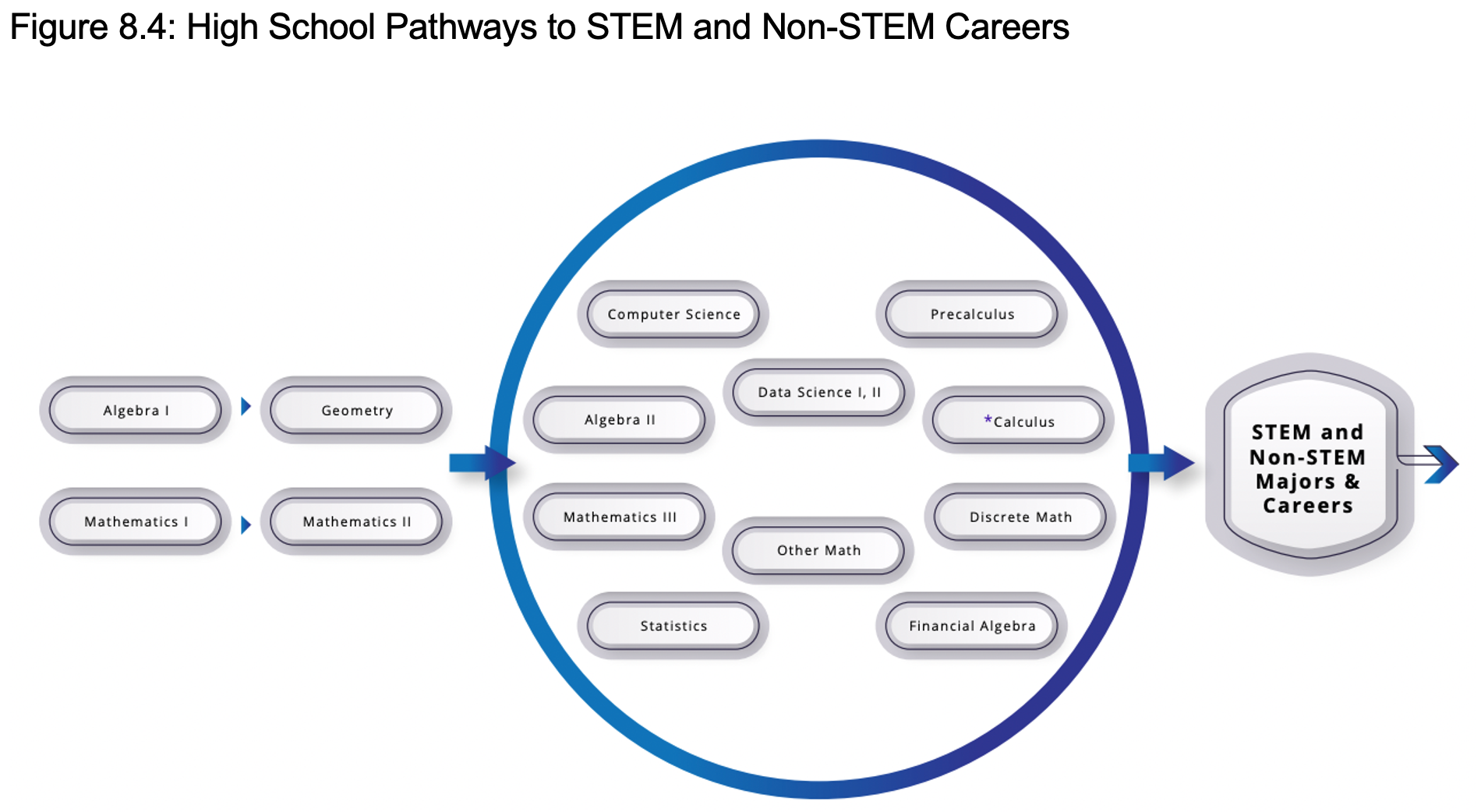
School districts have considerable latitude to design third- and fourth-year courses, and the framework cites Financial Algebra, comparable in rigor to Algebra II, where students do mathematical modeling related to personal finance. Another is Transition to College Math and Statistics (PDF), which Stevenson designed in partnership with Los Angeles Unified. It provides math practices, like reading and interpreting data from two-way frequency tables and bar graphs, for high school seniors uncertain of their plans for college.

The goal should be flexibility, keeping students’ options open. The framework cites examples of students’ journeys: A student who plans to major in non-STEM graphics arts discovers an interest in software applications, so she takes Pre-calculus as a senior with a support class, setting herself up for freshman calculus and programming classes. After the standard first two years of math, another student who plans to work in a fabrication shop after graduation takes a course in modeling to understand the math of three-dimensional printing.

High school sequences have drawn the most contention, but it’s the underlying instructional strategies that could create the framework’s biggest impact. The approach, which academics call constructivism, underlies the math standards that were adopted in California in the early 1990s, then abandoned after a grassroots revolt in 1997. While the changes wouldn’t be new, they could be drastic, fundamentally turning classroom instruction on its head.

The framework defines the difference in contrasting the beliefs in “unproductive” and “productive” roles of teachers.

The former, found in many classrooms, is “to tell students exactly what definitions, formulas, and rules they should know and demonstrate how to use this information to solve mathematics problems. The role of the student is to memorize information that is presented and then use it to solve routine problems on homework, quizzes, and tests.”

The latter should be “to engage students in tasks that promote reasoning and problem-solving and facilitate discourse that moves students toward shared understanding of mathematics. The role of the student is to be actively involved in making sense of mathematics tasks by using varied strategies and representations, justifying solutions, making connections to prior knowledge or familiar contexts and experiences, and considering the reasoning of others.”

Connecting to the world around them

Math isn’t working for the majority of students, the framework says, because there’s no context or connection with what they learn from one day to the next or to the world around them. A year is divided into units of “power standards,” which are taught individually, demonstrated with a procedure, and then assessed, before moving on to the next one.

The alternative is to tap into students’ curiosity with the goal of building deep understanding of math ideas. Classes should start with student-based questions about math and explore from there. Teachers should anchor lessons to “big ideas” in each grade that connect clusters of standards within the topic, like number sense, and across domains to show how algebra relates to geometry. Big ideas in third grade include fractions as relationships and number flexibility to 100; in sixth grade, they include relationships between variables.

“The framework is saying that we really need to make sure that the conceptual precedes the procedure to provide the understanding, so that when we get to those steps later on, we understand the why behind it. It’s not a mystery any more,” said Sampson.

A teacher might start off this way, said Stevenson: “Here’s the situation: What do you notice and wonder about it? Here’s a bunch of things that we’re going to talk about today. Which ones do you already know?” Answers will lead to procedures needed to solve it, whether how to do two-digit multiplication or to calculate the volume of a cylinder.

“Just the idea of the big ideas is huge, so that teachers aren’t feeling they’re teaching things in isolation,” said Vicki Murray, a learning coordinator in Buellton Unified who has taught elementary grades math, agrees. “Jo Boaler has really done an amazing job showing the mile-high view, that this idea connects to all these different other pieces of math.” Buellton is a 600-student district north of Santa Barbara.

“A lot of K-6 teachers are super excited about it, and it makes sense to them,” Stevenson said. “It’s actually asking them to teach math the same way they teach a lot of other things,” like the Next Generation Science Standards. But high school teachers may feel disoriented with the approach and burdened by the complex set of rubrics around which teachers should design lessons.

“I support the idea that we need to teach differently. I do agree that what we’re doing right now is not working. We’re trying to teach too much too fast,” Stevenson said. “I wonder if there isn’t a simpler formulation of what they (the authors) are trying to get at.” At the end of a class, she said, students may walk away with a “muddy sense of what they were to have learned.”

Tom Loveless, an education researcher who now lives near Sacramento, a former senior fellow at the Brookings Institution and the author of a book on the Common Core standards, gave a harsh assessment of the framework’s philosophy. The authors, he said, created a “false dichotomy” about the need for “conceptual understanding before procedural fluency. Good teachers teach both.”

The math framework should be organized around the content of the Common Core standards, not around “rather fuzzy ideas about process,” he said.

He said he is sympathetic with the critics that math facts and procedures have been taught poorly. “But there will be a toll paid for pushing them in the background.”

“The previous framework was very clear that math fluency involves speed and accuracy. The proposed framework rejects speed as being even part of fluency, and that’s a problem,” he said.

Math facts learned and stored in long-term memory can be retrieved effortlessly when students take on more-complex cognitive tasks, he wrote in a recent article. Contrary to the requirements of the Common Core standards, the framework calls for pushing back fluency in multiplication and division tables until late elementary grades. The delay will carry forward, and he expects fewer students will be prepared for algebra in ninth grade.

That has been the experience of Jane Molnar, who has been teaching math for 43 years as a math specialist working in classrooms and as a tutor. “If you don’t master certain things in first grade, second grade, third grade and instead you’re just exploring and talking about numbers, kids just can’t keep up. And when the same thing continues through middle school, students who wouldn’t know how to divide with ease using the division algorithm would find trying to divide polynomials in algebra way too complicated.”

Training is essential

Advocates of the framework agree that intensive training will be critical and a heavy lift for teachers who lack strong content knowledge.

“There’s going to be some discomfort for sure at the front end for those who really have a very regimented routine about how math should be taught,” said Sampson.

Brown said his biggest hope is that the framework “will really influence the way that teachers think about teaching and engaging their students.” His biggest fear is that “the state will not really fully fund the rollout and provide teachers with the support they need to really implement it.”

Like Brown, the framework’s original authors said the payoff would be huge.

“One of the missions of this framework is to get rid of ways of thinking that only some students can do mathematics to high levels and open up this beautiful subject of mathematics for everyone,” said Boaler.

Ben Ford, a math professor at Sonoma State University, said, “If my students start arriving at university understanding mathematics as a set of lenses for exploring questions that they’re actually interested in, I would be ecstatic. And that is one of the goals of this framework.”

Loveless, however, predicts history will repeat itself.

Just as more parents now are demanding an end to whole-language instruction and adoption of reading curricula with basic literacy skills, parents seeing poor results in math will demand change in a few years, as they did in the ’90s, he said.

“Math facts are to math as phonics is to reading,” Loveless said.

This story was originally published by EdSource.